合作客戶/
拜耳公司 |
同濟大學 |
聯合大學 |
美國保潔 |
美國強生 |
瑞士羅氏 |
相關新聞Info
推薦新聞Info
-
> 不同質量濃度、pH、鹽度對三七根提取物水溶液表面張力的影響(三)
> 不同質量濃度、pH、鹽度對三七根提取物水溶液表面張力的影響(二)
> 不同質量濃度、pH、鹽度對三七根提取物水溶液表面張力的影響(一)
> 氟硅表面活性劑(FSS)水溶液表面張力、發泡力、乳化力測定(三)
> 氟硅表面活性劑(FSS)水溶液表面張力、發泡力、乳化力測定(二)
> 氟硅表面活性劑(FSS)水溶液表面張力、發泡力、乳化力測定(一)
> 不同配方的水性氟丙樹脂涂料涂膜合成、性能指標
> 芬蘭Kibron表面張力測試儀跟蹤氯乙烯懸浮聚合中的表面張力變化情況
> 泡泡消煙原理,不同質量分數堿劑發泡液表面張力的測試結果
> 什么是超微量天平,超微量天平使用方法、最小稱量值
?強子夸克相變的表面張力數值變化研究(二)
來源:物理學報 瀏覽 112 次 發布時間:2025-01-20
強子夸克相變的表面張力
對于一級相變,當體系的溫度達到相變臨界溫度時,模型的熱力學勢能具有兩個相等的極小值,并且這兩個極小值被一個勢壘分開。此外,由圖1可知,這兩個極小值所對應的σ場的真空期望值分別對應一個大的數值和一個小的數值。如果體系的溫度進一步降低,那么σ期望值較小的那個真空勢能將大于σ期望值大的那個真空勢能,此時我們把前面那個真空稱為亞穩態真空(通常稱為偽真空),而把后面那個真空稱為穩定真空(通常稱為真真空)。
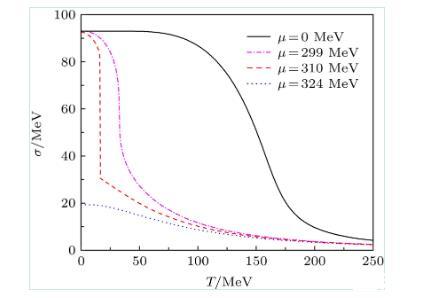
圖1在不同夸克化學勢密度條件下,σ場的真空期望值隨溫度的演化行為
在經典物理中,雖然偽真空的能量高于真真空,但是由于兩個真空之間還有一個勢壘,故偽真空無法回到真真空。但是,對于一個量子體系,由于存在量子隧穿效應,偽真空還有一定的概率可以回到真真空,從而發生一級相變,并把多余的能量以相變潛熱的形式釋放出來。為了準確地描述該一級相變的相變動力學過程,我們借助液滴核合成唯象模型來描述夸克強子的一級相變。
在液滴核合成唯象模型中,由于存在漲落,會產生一系列新的、能量較低的真真空的泡泡(通常用一個球形泡泡來模擬強子相),然后通過這些泡泡的膨脹最終實現從偽真空到真真空的轉變。具體的完成過程如下:由于偽真空的單位體積自由能密度高于真真空的單位體積自由能密度,泡泡在膨脹的過程中,體系的能量降低,但是,由于這些泡泡同時存在表面張力,又會束縛氣泡的膨脹,二者存在競爭關系。體積自由能與r3成正比,表面自由能與r2成正比,故存在一個臨界半徑rc,當r<rc時,表面自由能占主導地位,泡泡會最終收縮為偽真空,從而消失;而對于r>rc,體積自由能占主導地位,泡泡會一直膨脹直至占據整個系統,從而完成夸克相到強子相的完全轉變。
如果把真真空的泡泡看成是一個半徑為r的球形泡泡,那么體系總自由能的改變為
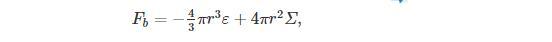
其中,ε為偽真空與真真空的單位體積自由能密度之差;Σ是泡壁的表面能量密度,即兩相界面的表面張力。
在偽真空的環境下,大小不一的真真空泡泡,由于量子漲落和熱漲落隨機出現并消失,直至泡泡的半徑大于等于臨界半徑,然后這些泡泡就會一直膨脹下去,完成一級相變的相變過程,并把多余的體系自由能以相變潛熱的形式釋放到環境中。基于這個機制,單位時間單位體積的臨界泡泡成核率可以表示為

其中,T為系統溫度。因子P通常比較難計算,為了計算方便通常采用簡單的量綱分析,用T4近似代替P.利用歐幾里得空間的有限溫度場論方法,上述的成核率可以從下面的歐幾里得拉格朗日密度出發:
這里為了方便討論,我們把熱力學有效勢能重新定義為Veff(σ)=Ω(σ,T,μ)。則體系的自由能表示為
為偽真空下的σ場的真空期望值。也就是說,遠離真真空泡泡的中心,體系處于亞穩態,相當于真真空的泡泡在偽真空中產生并膨脹。

對于一般有效勢Veff,在邊界條件(16)式下,通常不能通過解析方法得到(15)式的解析解,只能求助計算機得到該方程的數值解。但是,如果考慮真真空泡泡的尺寸比壁厚大得多的情況,或者偽真空與真真空的勢能差與介于兩個真空之間的勢壘相比小得多的情況,該情況也稱為薄壁(thin-wall)近似,則方程式(15)中的第二項與第一項相比可以被忽略,即方程進一步簡化為由此,一旦得到了體系的自由能Fb,就可以很容易估算出夸克強子一級相變的成核率Γ.
利用薄壁近似,圖2給出了當T=Tc時,夸克強子一級相變的表面張力隨夸克化學勢的變化。可知在一級相變區域,當化學勢增大時,強子相的表面張力也隨著化學勢增大。當溫度接近零時,強子夸克相變的表面張力約為12.6 MeV/fm2.在T→0的情況,本文理論預言與文獻一致,但該文獻只是考慮T=0的冷夸克物質的夸克強子一級相變。
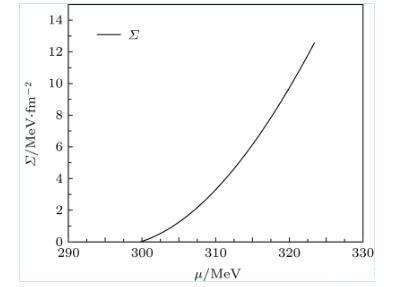
圖2 T=Tc時表面張力與夸克化學勢的演化關系
結論
利用兩個夸克味的夸克介子模型,在有限溫度、有限夸克化學勢密度條件下,本文計算了模型熱力學有效勢能,通過求解該熱力學有效勢能對σ場的變分,得到σ介子場的運動方程,求解該運動方程得到σ場的真空期望值隨溫度和密度的變化關系。我們發現,在高溫低密度區域,量子色動力學的相變是過渡相變,而在低溫高密度區域,量子色動力學的相變是一級相變,在過渡相變和一級相變的交界處存在一個相變的臨界點,我們稱之為CEP(critical end point)。為了提供更加完整的理論結果,不同于其他文獻,我們在模型的計算中考慮夸克場的真空漲落和重整化效應,并且我們采用了一套廣泛應用并被實驗認可的模型參數來計算。特別是夸克場的真空漲落效應,通常會使得一級相變的相變區域變得很小,從而進一步推低夸克強子相變的強子相的表面張力的數值,而很小的表面張力數值,使得中子星在早期演化過程中產生更加復雜的中子星結構,比如中子星的混合相的出現,夸克星硬層的出現等物理現象。
考慮到基于夸克介子模型的熱力學性質計算結果與當前的格點量子色動力學計算差距較大,與當前的實驗觀測也有相當大的出入,故在該模型中我們考慮膠子的自由度,把夸克介子模型進一步推廣到Polyakov圈拓展的Polyakov-quark-meson model(PQM)模型。由于考慮了Polyakov圈拓展,需要在模型中引入另外兩個序參量,因此PQM模型具有三個序參量,在計算夸克強子相變表面張力時,需要同時求解三個非線性微分方程組,理論和數值計算將變得非常復雜和困難,特別是在這種情況下,薄壁近似將不再有效,只能采用數值計算來獲得表面張力的數值信息。目前,該方向的研究正在進行中。










