合作客戶/
拜耳公司 |
同濟大學 |
聯合大學 |
美國保潔 |
美國強生 |
瑞士羅氏 |
相關新聞Info
-
> 兩種烷基咪唑亞磷酸酯離子液體熱穩定性、表面張力測定(三)
> 無機鹽對油/水界面張力及對油滴鋪展的影響規律
> 壓力、溫度、碳原子數及分子結構對CO2-正構烷烴界面張力的影響——實驗部分
> 新制備的雙向拉伸聚丙烯消光膜,具有高挺度、表面張力持久等優點
> 酚胺樹脂聚醚型破乳劑分子結構、濃度對油-水界面張力的影響——結果與討論、結論
> 超聲協同殼聚糖處理對蛋黃液界面張力的影響
> 表面張力儀在表面活性劑中的應用
> 接觸角遲滯時氣~液界面張力的溫度敏感性對液滴蒸發過程的影響——結果分析、結論
> 嗜熱鏈球菌發酵乳對全蛋液起泡性、pH、黏度、表面張力的影響(二)
> 泡沫豐富和清潔力好是一回事嗎?
推薦新聞Info
-
> Wilhelmy吊板法測試溫度、鋁元素和稀土元素對鋅浴表面張力的影響
> 基于表面張力系數等模擬液滴撞擊熱壁面的動力學行為(二)
> 基于表面張力系數等模擬液滴撞擊熱壁面的動力學行為(一)
> 10種常用表面活性劑水溶液的表面張力測定、泡沫的產生和測試(三)
> 10種常用表面活性劑水溶液的表面張力測定、泡沫的產生和測試(二)
> 10種常用表面活性劑水溶液的表面張力測定、泡沫的產生和測試(一)
> 雙鏈乳糖酰胺季銨鹽表面活性劑物化性能、應用性能及復配性能研究
> ABA型聚醚改性有機硅表面活性劑在不同溶劑中的泡沫性能的相關性
> 什么是超微量天平?超微量天平用在什么地方
> 表面能和表面張力關系,如何降低表面張力
基于表面張力系數等模擬液滴撞擊熱壁面的動力學行為(一)
來源:力學學報 瀏覽 18 次 發布時間:2025-02-21
液滴撞擊固體壁面是一種常見的物理現象,廣泛應用于噴墨打印、等離子噴涂、噴霧冷卻、金屬淬火和抑冰等領域。液滴與固體壁面的相互作用是影響上述應用的重要因素,如墨滴撞擊紙張的鋪展特性會影響噴墨打印的分辨率,液滴與壁面的接觸時間會影響噴霧冷卻的效率,而抑冰又要求減少液滴與壁面的接觸時間。類似的情況還有許多,盡管很多學者已經開展了大量研究,但液滴與壁面的相互作用仍因其復雜性與多樣性而未被全部知曉。
對于液滴撞擊固體壁面,通常從兩方面展開研究,即液滴的鋪展特性與傳熱傳質特性。學者們圍繞這兩方面進行了一定研究。隨著越來越多的動力學及傳熱學特性被發現,研究工況的溫度也隨之升高,其中一個研究方向逐漸聚焦于高溫情況下顯著的液滴撞擊特征,Leidenfrost現象。1756年,Leidenfrost提出了這一標志性的液滴撞擊高溫壁面特征,開創了新的研究領域。Leidenfrost現象是液滴受到高溫壁面的影響,氣液快速交換熱量,液滴底部產生蒸汽膜的物理現象。蒸汽膜厚度受多種因素影響而不斷發生變化,并存在程度不一的振蕩情況。實驗結果表明,Leidenfrost現象中液滴底部蒸汽為徑向的層流流動,并有學者對蒸汽層的擴散提出了相關預測模型。
除底部氣膜外,Leidenfrost現象下液滴的動力學與傳熱特性也與其它工況不同。首先,達到Leidenfrost狀態需要有足夠高的溫度,這一溫度通常被稱為Leidenfrost點,其大小受到壁面粗糙度,重力和表面張力等因素的影響。其次,液滴撞擊壁面的We數較大時,相對于未加熱壁面與濕壁面,Leidenfrost狀態下液滴更容易發生破碎。當液滴開始鋪展時,由于液滴與壁面間的蒸汽膜存在,壁面粗糙度與接觸角對液滴鋪展的影響被削弱,這使得Leidenfrost狀態下的液滴鋪展情況大于膜態蒸發和核態沸騰狀態下的液滴鋪展情況,且液滴的最大鋪展情況與脫離時間仍然由We數決定。
雖然,很多學者對Leidenfrost現象進行了一定研究,但是大部分研究成果聚焦于高溫平面上的液滴動力學與傳熱特性,而非平面上Leidenfrost現象的研究非常有限。但是,液滴撞擊高溫曲面廣泛存在于電子工程、機械工程、動力工程、化學工程等領域。如液滴撞擊高溫球面,常見于流化催化裂化和流化焦化等工藝,這一過程影響著多種過程系統的性能,尤其是對于生產更有價值的汽車燃料具有重要意義。鑒于此,本文進一步探究液滴與高溫球面撞擊過程中液滴的Leidenfrost現象,采用數值模擬方法進行研究,使用Fluent軟件構建了二維軸對稱數值模型,采用VOF模型及Lee模型,分析液滴撞擊高溫球面的動力學特性與傳熱特性,探討Leidenfrost現象的機理及各因素的影響規律。
1.模型及方法
1.1物理模型
液滴撞擊球面的物理模型如圖1所示,半徑為r的球狀液滴以初速度v撞擊半徑為rn的固體球面,并在球面上鋪展、收縮和反彈。液滴材料為水,考慮重力加速度的影響,液滴與壁面撞擊時t=0.
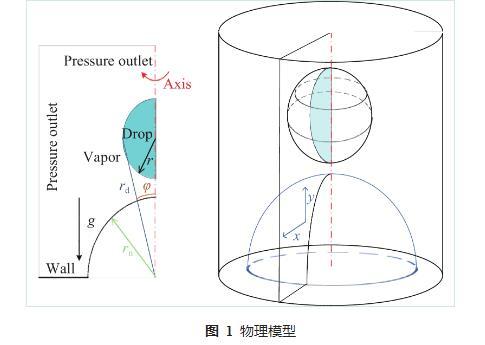
圖1物理模型
定義無量綱系數鋪展因子β

式中:rm為液滴鋪展半徑,mm.鋪展系數β可以直觀地反映液滴在壁面上鋪展變化的規律。鋪展系數越大,說明液滴鋪展越充分。
與撞擊平面不同,液滴撞擊球面時會沿球面鋪展,因此鋪展半徑rm的定義與平面有所不同
(2)
式中,φ為液滴鋪展角度,rd為液滴鋪展最大處與球心間的距離。
1.2控制方程
為了模擬液滴撞擊熱壁面的動力學行為,需要求解連續性方程、動量方程與能量方程,假設氣液兩相均為不可壓縮流體,表面張力系數、密度、粘度、導熱系數和比熱等物性參數均為常數
式中,u為速度矢量;ρ為流體密度;S為相變引起的質量源項;μ是流體黏度;g為重力加速度;Fσ為表面張力;T為流體溫度;Cp為定壓比熱;k為導熱系數;Se為相變引起的能量源項。
1.3 VOF模型
VOF模型是一種兩相流動計算模型,其通過計算網格中相的體積分數以捕捉兩相的分界面,對于目標流體,流體體積函數C可表示為

流體體積函數滿足的輸運方程為
采用隱式格式求解流體體積函數方程,并包含隱式體積力,界面建模為sharp模型,采用的界面捕捉算法為Compressive方法。
兩相流體的密度ρ、黏度μ、導熱系數k的計算式為
式中,下標l、v分別表示液相和氣相。
采用CSF模型計算表面張力,表達式為
式中,σ為表面張力系數;n為界面法向;κ為界面曲率。
1.4 Lee模型
本文采用Lee模型模擬氣液相變過程,控制方程為

式中,αv為氣相體積分數,uv為氣相速度,
和為蒸發和冷凝的傳質率。對于蒸發過程,傳質表達式為
式中,αl為液相的體積分數;Tl為流體溫度;Tsat為飽和溫度;Acoeff為控制相變強度的因子,可以表示為
式中,db為液體蒸發時產生的氣泡直徑;χ表示液體表面吸附蒸氣分子的量,為調節系數;M為摩爾質量;R為通用氣體常數,8.314 J/(mol·K);L為蒸發潛熱;在本文中,Acoeff取值為500.
1.5網格無關性驗證
為了選擇合理的網格精度,首先開展網格無關性驗證。同時,為了驗證數值模擬的準確性,也需與實驗結果進行對比驗證。本文以文獻中的工況為基準,采用異丙醇作為液相,展開網格無關性驗證與模型驗證。計算區域的尺寸為5 mm×8 mm,液滴初始溫度為355.65 K、初始直徑為1.61 mm、液滴撞擊速度為0.348 m/s、We數等于8.6、球體直徑為10 mm、壁面溫度為623.15 K、壁面接觸角為67°、重力加速度為?9.81 m/s2.其它流體物性如表1所示。
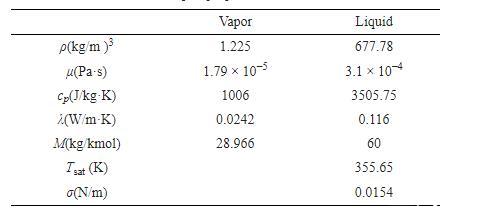
表1流體物性參數表
為了定量分析網格數量對數值模擬結果準確性的影響,以液滴撞擊壁面時的鋪展因子作為定量分析指標及網格無關性驗證的評判標準。網格數量從36 w開始增加,每次增長大約30 w,并繪制液滴鋪展因子β隨時間變化與網格數量的關系圖。如圖2所示,網格數在86 w以上時基本不會對模擬結果產生影響,為保證模擬精度并確保求解時間,本文采用86 w網格數作為模型的基準網格數進行模擬。從圖中也可以看出,數值模擬結果與參考文獻中的實驗結果趨于一致,說明本文采用的模型可以用于研究液滴撞擊球面的Leidenfrost現象。
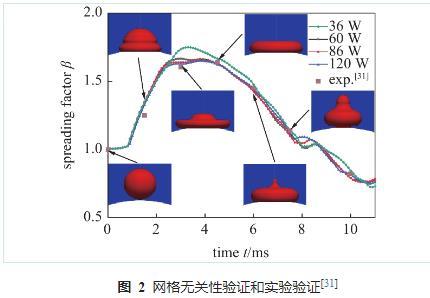
圖2網格無關性驗證和實驗驗證
圖3進一步給出了不同時刻液滴撞擊球面的形態變化,圖3(a)為二維模擬結果、圖3(b)為文獻的實驗結果、圖3 c為paraview處理后的三維化模擬結果。如圖所示,0 ms時刻,液滴以0.348 m/s的速度撞擊球面,隨后液滴由慣性力驅動開始鋪展,鋪展過程中動能不斷轉化為表面能和耗散能。1.5 ms-4.5 ms時段,液滴由球狀逐漸轉變為圓盤狀。達到最大鋪展系數后,表面張力促使液滴回縮,6.0 ms-7.5 ms時段,液滴逐漸回縮并開始反彈,上下部分出現較明顯分界,整體呈葫蘆狀。10.0 ms時,液滴與壁面的接觸面積明顯減少。15.0 ms時,液滴與壁面完全分離。可以看出,模擬結果與實驗情況吻合良好,進一步證明本文數值模擬的準確性。
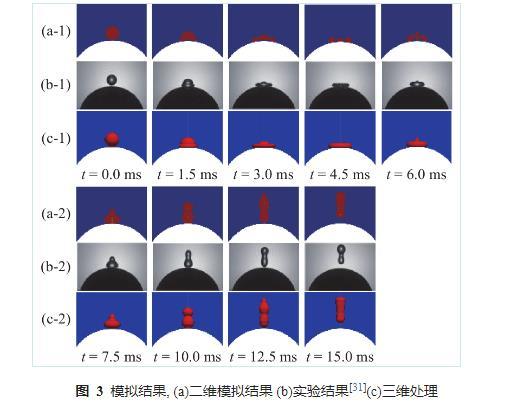
圖3模擬結果,(a)二維模擬結果(b)實驗結果(c)三維處理










